1.-¿De dónde viene?

Algunos piensan que viene de algún tipo de rito ancestral para torturar a la gente o que se corresponde con algún tipo de práctica sadomaso, pero no, esta prueba existía antes de la publicación de 50 sombras de Grey. Como sus primos, el de razonamiento verbal y abstracto, es la prueba perfecta para estimar tu capacidad de razonar numéricamente, es decir, saber usar los números y hacer los cálculos pertinentes para resolver ciertos tipos de problemas. Por supuesto, sirve para demostrar que: ¡AUNQUE SEAS DE LETRAS!  ¡PUEDES SACARLO ADELANTE!

2.-¿De qué va?

Básicamente tienes 10 preguntas-problemas, a responder en 20 minutos, donde te dan una serie de datos. Puede ser en formato tabla, quesitos o tarta, gráficos o simplemente dentro del texto, en los cuales tendrás que responder a una pregunta con respuesta numérica. La respuesta podrá ser un valor, una relación/proporción o un porcentaje.

3.-¿Dónde está la trampa?

Haciendo números (chiste fácil, exacto como estos test, aunque no te lo creas). Digamos que contamos con tres trampas para los candidatos :

1.-Pensar «yo es que soy de letras y se me dan fatal los números».- A ver, alma de tortilla francesa sin sal, te podemos dar la respuesta evidente “Y los de ciencias (nuestra croqueta lo es) sabemos escribir, mejor o peor, pero escribimos”. Otra opción es la sargento de hierro : «Nada de lloros, depresiones o resoplidos, esto puede sacarlo cualquiera… con ganas de aprender y esforzarse.» (Sin echarle un poco de ganas no lo saca nadie, que no te lo regalan tampoco).

2.-Lo numérico es difícil – ¡ERROR! Ni es difícil ni se trata de números, se trata de razonamiento. Los números/operaciones van al final. Son una consecuencia, no el fin del problema.

3.-La calculadora es mi mejor amiga – ¡FALSO! Es tu enemiga. Preparada para pegarte una puñalada trapera en el examen. Se trata de saber qué tienes que hacer  respecto a la pregunta y tener todo bien identificado: los datos y el camino a la solución. Sólo en ese momento, es cuando te pones a calcular con ella, no antes. Lanzarte a operar como un mono de manera aleatoria te da tantas posibilidades de sacar el problema como de componer «Hamlet» aporreando un teclado aleatoriamente.

4.-¿Qué conocimientos previos necesito?

Pues los básicos de matemáticas: saber sumar, restar, multiplicar y dividir.  En cuanto a las operaciones, no habrá nada más complicado que eso. Pero conviene que puedas operar mentalmente de manera ágil.

Otros elementos que conviene que domines  :

• Potencias, órdenes de magnitud y unidades de medida
• Operar con fracciones
• Operar porcentajes
• Interpretar gráficos

Si te sientes un poco perdido, sin problema, sigue leyendo que ahora te hablamos del tema.

5.-Potencias, órdenes de magnitud y unidades de medida

A.-Potencias

Algo sencillo, se trata de un número  (la base) acompañado de un exponente y se traduce por multiplicar la base tantas veces por sí misma como indique el exponente.

5³ =5*5*5

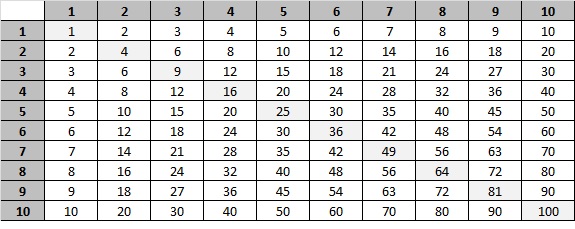
B.-Tablas de multiplicar

No por conocidas, son menos importantes y conviene saber manejarlas con soltura.

 C.-Órdenes de magnitud

Esto es especialmente importante dominarlo cuando estamos utilizando números altos, por ejemplo: miles o millones de algo. Saber quitarte de en medio  ceros(000) al operar es algo que puede resultar muy útil. Recuerda que el tamaño… de los ceros, mejor dicho, su longitud, importa.

No es lo mismo 100  que 1.000.000, pues uno es 10²  y el otro 10⁶

D.-Las unidades

Vale que en Europa usemos el Sistema Internacional de unidades (metro, gramo, segundo) pero hay que conocer las equivalencias entre uno y otro, ya que el diablo está en los detalles. Y siguiendo con los dichos, aquí va otro que se aplica a las unidades: “No mezclar churras y merinas.  Opera siempre churras con churras y merinas con merinas”. ¿Qué quiere decir esto?

Por ejemplo: La renta percapita que viene en unidades como  € /persona , no puedes, por ejemplo, sumarle una cantidad de personas o de dinero.

• 500 €/pc   + 500 €   = ERROR
• 500 €/pc   + 3 personas = ERROR
• 500 €/pc  *  3 personas  = 1500 €

La última es correcta porque si pensamos que tenemos 500€ por cada persona, si tenemos 3 personas , totalizamos 1500€.

¡FIJARSE! Las unidades de superficie o volumen no se operan linealmente. Es decir, para pasar de metros a  decámetros, se trata de dividir entre 10, si fueran kilómetros sería entre 1000. ¿Pero y si es una superficie? Cada salto de unidad que deis, deberéis multiplicar o dividir por 100 y si es volumen por 1000. Es decir:

• 1000 metros = 1 km
• 1000 metros² = 1000 / 1000 000 = 0.001 km²
• 1000 metros³ = 1000 /  1000 000 000 = 10³ / 10⁹ = 0.000001 km³

E.-Fracciones

Una fracción no deja de ser un número partido por otro, así dicho en grueso. Lo que hagas con ellos es cosa tuya y de lo que te pidan en el problema, así que ve secando esos sudores que te recorren la espalda.

La fracción suele ser una interpretación, por ejemplo, de los trozos de tarta que te comes, Si divides una tarta en 8 porciones y te comes 2, tendrás  que te has comido 2/8 de tarta.

F.-Propiedades y operaciones con las fracciones

Equivalencia

son equivalente si  A*D = B * C

Suma y resta  de fracciones

 Y si el divisor es distinto haríamos el mínimo común múltiplo. Es decir:

1. Se cogen los divisores
2. Se descomponen
3. Los números que se repitan se descartan
4. Se multiplican los demás y el resultante pasa a ser el nuevo divisor
5. Los dividendos se multiplican por el resultado de dividir el mcm entre el divisor de esa fracción

Multiplicación

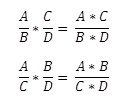
Recuerda: que las letras no te impidan ver el bosque …¿Eh? Vale, dejamos la poesía y lo decimos clarito: juega con la formula, cambia las letras por números y prueba a ver qué sale.

Y división

Recuerda «divide y vencerás» que decía Julio César … vale, dejamos la  historia y lo decimos clarito: juega con la formula, cambia las letras por números y prueba a ver que sale.

G.-Porcentajes

Los porcentajes en realidad son fracciones. En concreto una fracción de cien (100).

Si algo crece un % en un tiempo dado, por ejemplo, el PIB de 2009 es de 350 millones y en 2010 ha crecido un 5% se calculará:

PIB(2010) = PIB(2009) * (1 + 5%) = PIB2009 (1 +0.05) = PIB2009*1.05 = 367.5 millones

Recuerda que los porcentajes no se pueden operar a lo bruto, hay que pasarlos a decimales, por ello 100% es equivalente a 1 y un 20% lo será a 0,2 para operar. En elejemplo el 5% es 0.05.

Y de forma evidente, la fórmula que acabamos de usar un poco antes es la que sigue :

Del mismo modo, de esa fórmula se puede deducir la que nos permite calcular el % de diferencia existente entre 2 cifras o magnitudes.

¡OJITO! con algunas propiedades y detalles en torno a los porcentajes

1.-Sobre una cantidad, una subida de un % y luego una bajada, o a la inversa, no son equivalentes. Si tenemos 100 unidades de algo y :

• aumenta un 10% tendré 110
• si disminuye 10% = 99

2.-No confundir los porcentajes y los puntos porcentuales. Los puntos porcentuales  se pueden sumar o restar directamente, los % de crecimiento y decrecimiento son modificaciones relativos.

3.-Si un alza de un X% se repite en el tiempo Y, usamos la siguiente fórmula para calcular todo el % acumulado :

%=(1+X%)^Y-1

es decir el crecimiento anual de la economía fue del 3% durante 4 años, NO es 4*3%, sino (1+3%)⁴-,1

4.-No se pueden sumar dos crecimientos % . Si a un crecimiento del 5% le sigue uno del 6%, no será uno del 11%. Sino qe sobre 100 unidades, primero tendremos el 5%, lo que nos da 105, y luego le aplicamos el 6% (lo que nos da 6.3) = 111,3.

5.- Los % sí son conmutativos – Un Y% seguido de otro X% será igual que un X % seguido de otro Y%.  Te lo ponemos en un gráfico para que no te líes.

Partiendo de una cifra de 200 unidades (de lo que sea) vamos por un camino que le añade un 15% y  para quitarle a continuación el 15% y  otro que empieza quitandole 15% y luego se lo añade. ¿Cuál será la cifra final en ambos casos? ¡Sorpresa! Es la misma, pero no así las cantidades sustraídas o añadidas, fíjate bien.

H.-MEDIAS

Aquí tenemos 2 tipos, la simple y la ponderada.

• Simple o aritmética – Si tengo 40 cromos y 5 niños ¿Cuántos cromos puedo repartir por niño? 40/5  = 8 cromos/niño
• Y la ponderada -En una granja tengo 10 gaillnas que pesan 2kg cada una y 5 lechones de 20 kg ¿Cuál es el peso medio de los animales de la granja?

10 gallinas* 2 kg + 5 lechones * 20 kg = 120 kg

Se divide entre todos los animales, es decir, 15, y tenemos  un peso medio de 8,5 kg/animal.

I.-La regla de 3

La regla de 3 es un método de cálculo que os permite extrapolar un número o una información. Si para hacer un jersey necesito 5 ovillos de lana, con 30 ovillos, ¿cuántos jerséis puedo tejer?

6.-Reglas de redondeo

Las reglas del redondeo son las siguientes:

• Si el primer dígito a eliminar es mayor o igual que 6, se redondea hacia arriba.
• Si el primer dígito a eliminar es menor o igual que 4, se redondea hacia abajo.
• Si ese dígito es un 5 seguido de algo (ver indicaciones más abajo), se redondea hacia arriba.
• Si es un 5 justo (es decir, seguido de ceros), se redondea hacia el par superior o igual. Es decir, si es un par se queda como está, si es un impar, se redondea hacia arriba.

Esto también puede usarse para redondear números más altos. Imagina que las potenciales soluciones son 5000, 7000, 9000 y 11000. Y operando tienes números tales como 39, 95, 64 y 47. Puedes redondearlos a 40, 100, 60 y 50 para operar más rápido.

7.-¿Tablas o gráficas?

¿Tiene cara nuestra croqueta de que le importe el formato? ¿Qué más da? Las dos pueden contener la misma información pero con distinto formato. Echa un vistazo a la siguiente tabla y al gráfico. ¿Dónde está la diferencia?

 También podemos tener tablas con toda la información

En esa tabla tenéis los detalles del paro juvenil (personas entre 19 y 25 años) en % respecto a la población  total de esa edad.

Gráficas mixtas con información repartida

En estas gráficas, la tarta te indica el % de cada fuente de combustible y la columna de abajo las toneladas de cada combustible.

Gráficas con toda la información

En esta gráfica tienes la distribución por edades y sexos de la gente que ha presentado tesis doctorales en un año determinado.

8.-¿La estrategia ganadora?

Ahora que entramos en materia que quede clara una cosa, se trata de entender la pregunta no de ser el más chulo del barrio operando. Así que sabiendo operar, ¿cómo lo hago para resolver el problema?

1.-Lee la pregunta

2.-Razona lo que te están preguntando  ¿Lo has identificado correctamente? Ojito con las unidades, a veces los datos te vienen dados en unas unidades (o moneda/divisa) y la respuesta te la piden en otras unidades (o moneda/divisa)

3.- Plantea la solución, ¿qué cálculos necesitas? ¿Realmente necesitas esas operaciones? A veces saber gestionar bien los númerod te permite ahorrar operaciones = ahorrar tiempo. Puedes apuntarte los pasos en las pizarra que te dan. Vale, no te dan borrador, pero puedes usar el dedo en caso de necesidad, al acabar te limpias y punto.

4.-Calcula. Lo estás deseando, te quema los dedos y ahora es es el momento de usar la calculadora y ponerte a buscar tu resultado.

5.- Comprueba que tu solución coincide con las que te dan . Lo bueno del test numérico es que la solución es cierta si has hecho bien los pasos anteriores pero, ¿y si no te coincide? Bien, dos opciones:

• Te has equivocado en el razonamiento
• Te has equivocado en el cálculo

6.-Si los pasos anteriores los has hecho con detalle, te debería resultar sencillo repasar y verlo Si al repasarlos ninguno te da el valor correcto, entonces es que tienes que volver al punto 1.

7.-Última consideración. Si has invertido más de 1,30 minutos en los pasos anteriores y tienes que volver al punto 1, sin la seguridad de haber encontrado el fallo, mejor pasa al siguiente problema y ya volverás.

9.-Últimos consejos, pero no menos importantes:

• Aprovecha el tiempo que tienes antes de iniciar el test para familiarizarte con la calculadora. Tienes hasta 15 minutos para ello. Repasa todas las funciones, coge confianza con ella y verás que eso también te aporta tranquilidad para los test que están por venir.

• Si te atascas en un problema: ¡Sáltatelo! Y vuelve luego, mejor dejar 1 sin contestar, que por intentar resolver uno, dejar 4 sin contestar. Recuerda que este ejercicio en la mayoría de las convocatorias es un pasa/no pasa, todo lo que sea más de un 5 solo suma para tu orgullo.
• ¿Un número es divisible por otro? sí, cuando el primero al ser divido por el segundo da como resultado un número entero. Y como nunca está de más saber los números que son divisibles y sus reglas
  • Un número es divisible por 2 si el último dígito es 0,2,4,6,8
  • Un número es divisible por 3 si la suma de los dígitos es divisible por 3
  • Un número es divisible por 5 si el último dígito es 5 ó 0.
  • Un número es divisible por 9 si la suma de los dígitos es divisible por 9
  • Un número es divisible por 10 si el último dígito acaba en 0.

10.-¿Algún ejemplo para practicar?

Seguro que es lo que te está pidiendo el cuerpo ¡práctica! ¡práctica! ¡práctica! Bueno si es sábado noche a lo mejor está pidiendo otra no tan numérica con tu media croqueta … o si…ejem, nos centramos en lo que toca, aquí os dejamos unos ejercicios para que deis al relleno neuronal.

Ejemplo 1

Dados los siguientes datos:

1. ¿Cuál tiene más densidad de población?
2. ¿Cuál tiene mayor GDP per capita?
3. ¿Cuál tiene el mayor volumen en la balanza de pagos?

Ejemplo 2

La gráfica muestra la edad de presentación de la tesis doctoral. En la universidad, se considera que aquellos que  tenían menos de 30 años cuando presentaron la tesis han realizado tesis+carrera. Si 14706 presentaron su tesis en este año, de los cuales el 51% eran mujeres.

1. ¿Cuántos fueron los que hicieron tesis+ carrara?

1. ¿Cuál es la relación entre hombres y mujeres de 30-39 años, que presentan la tesis

1. ¿Qué porcentaje de hombres, entre 40 y 55 años, respecto al de mujeres presentaron la tesis?
2. ¿Cuántos hombres y mujeres presentaron la tesis con una edad de 35 a 39 años?

¿Algo más?

Bueno y si nos hacéis un poco la pelota, tal vez subamos algún otro ejemplo 😉 Así que no olvidéis darle al like en Facebook, seguirnos en twitter o instagram y mandarnos un jamón (esto último opcional pero altamente recomendable).

Además, si os apetece rebozaros en el conocimiento epso-croquetil de YSE (tenemos el método más sabroso)  y profundizar en el tema. De vez en cuando organizamos cursos presenciales y online. Toda la info de los cursos aquí . y para más info, podéis  escribirnos a yasemoseuropeos@gmail.com

AVISO nuestros cursos son  para afrontar el examen CBT , no para hacer croquetas. ¡Que nadie se lie!

REGALO – Si has llegado hasta aquí, te mereces un pequeño regala y aquí lo puedes descargar , nuestras soluciones de los ejercicios de Test numérico de EPSO.  Aquí teneis el document con la Solución numérico test-web EPSO por YSE .

Por último, si os apetece seguir leyendo, aquí tenéis nuestros post sobre :

• El test cbt
• Razonamiento verbal
• Razonamiento abstracto
• Razonamiento situacional

Y si quieres saber de las fases siguientes

• Assessment Centre